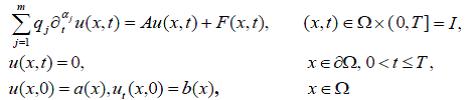The respected Comrade
"Scientific and technological strength is a state's most important strategic resource and a powerful propellant for social development."
Recently fractional differential equations have become an efficient tool for modeling complex nonlinear phenomena in fluid mechanics, life science, hydrology, geophysics and biology system and their mathematical aspects have been extensively investigated.
We studied the initial-boundary value problem for the multi-term time fractional wave equation modeling the flow of viscoelastic fluid with the fractional Maxwell constitutive relation:
Sakamoto and Yamamoto[JMAA, 382 (2011) 426-447] used the eigenfunction expansion to prove unique existence, continuous dependence on data and long-time behavior of weak solutions of initial-boundary value problems for the single-term time fractional wave equation corresponding to the case of m=1 in the above equation. Guidetti[JMAA, 476 (2019) 637-664] established the maximal regularity result in the space of Hölder continuous functions for initial-boundary value problems of the single-term time fractional wave equation. Also, Kian and Yamamoto[FCAA, 24 (2021) 168-201] proved the existence and uniqueness of weak solutions of initial-boundary value problems for the single-term time fractional wave equation when the source term belongs to the negative order Sobolev space.
In the case of m>1 we studied the existence and the asymptotic behavior of weak solutions of initial-boundary value problems for the single-term time fractional wave equation. First, by defining the weak solution by the Laplace transform, the existence and uniqueness of weak solutions was proved under some weak assumptions on initial condition, boundary condition and source term. In order to establish the well-posedness of initial-boundary value problems for the single-term time fractional wave equation, we improved the property about the boundedness of the multivariate Mittag-Leffler function obtained in [AMC, 257 (2015) 381-397]. Also, the Lipschitz stability of the solution with respect to the parameters of the equation was proved. Finally, we derived the H2-decay estimate of weak solutions of the initial-boundary value problem without source term.
Our research result was published in "Fractional Calculus & Applied Analysis" under the title of "Initial-boundary value problems for multi-term time-fractional wave equations" (https://doi.org/10.1007/s13540-022-00080-w).