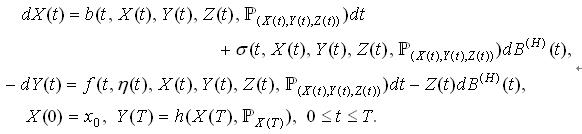정-역방향확률미분방정식에 대한 연구의 동기는 2가지로 볼수 있는데 하나는 확률조종문제의 최대값원리에서 공액방정식과 관련하여 처음으로 제기되였고 다른 하나는 비선형역방향확률미분방정식의 적합풀이가 어떤 준선형포물선형편미분방정식에 대한 풀이의 확률적표시로 리용될수 있다는것이 발견된것과 관련된다.
선행한 연구들에서는 표준브라운운동(백색잡음)에 관한 정-역방향확률미분방정식의 풀이의 성질들이 주로 연구되였다. 또한 전자공학, 금융수학, 천문학, 수문학실천에서 제기되는 초고주파교란계, 장기기억성을 가진 계를 묘사하기 위한 수학적모형으로서 분수브라운운동(유색잡음)이 출현하였는데 그것이 가지고있는 장기기억성, 자기상사성과 같은 흥미있는 성질들로하여 분수브라운운동에 관한 확률미분방정식에 대한 연구가 진행되였는데 지금까지는 정방향확률미분방정식 및 역방향확률미분방정식의 연구가 련립되지 않은 형태로 진행되였다.
분수브라운운동에 관한 정방향 및 역방향확률미분방정식이 련립된 경우의 연구는 분수확률조종계의 최대값원리에서 공액방정식의 풀이와 관련하여 제기되였는데 분수확률변환공식을 적용하는 과정에 확률도함수항의 처리에서 나타나는 일련의 난점으로하여 지금까지 미해결로 되여있었다.
우리는 분수브라운운동에 관한 련립평균마당 정-역방향확률미분방정식을 처음으로 제기하고 연구하였다.
연구에서는 이른바 《련속법》을 리용하는데서 파라메터 θ∈[0, 1]에 대한 분수평균마당 정-역방향확률미분방정식을 제안하고 방정식의 풀이가 존재하는 새로운 공간을 구성함으로써 연구에서 제기한 완전련립분수평균마당 정-역방향확률미분방정식의 풀이의 유일존재성과 비교정리, 풀이의 약단조성과 맆쉬츠련속성을 증명하였다.
우리의 연구결과는 잡지 《Brazilian Journal of Probability and Statistics》에 《Properties of solution for fully coupled fractional mean-field forward-backward stochastic differential equation》(https://doi.org/10.1214/24-BJPS596)의 제목으로 출판되였다.