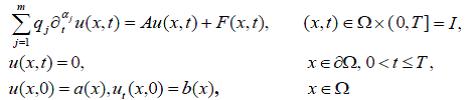《과학기술력은 국가의 가장 중요한 전략적자원이며 사회발전의 강력한 추동력입니다.》
최근에 분수계미분방정식은 류체력학, 생명과학, 수문학, 지구물리학, 생태계리론 등에서 나타나는 복잡한 비선형현상들을 모형화하는데서 효과적인 수단으로 되고있으며 그것에 대한 수학적연구도 깊이있게 진행되고있다.
우리는 분수계막스웰구성관계를 가진 점탄성류체의 흐름을 모형화하는 다항시간분수계파동방정식의 초기경계값문제
를 연구하였다.
선행론문 [JMAA, 382 (2011) 426-447]에서는 우의 방정식에서 m=1인 경우에 해당되는 단항시간분수계파동방정식에 대하여 고유함수전개를 리용하여 초기경계값문제의 약풀이의 유일존재성과 자료에 관한 풀이의 련속적관련성, 풀이의 긴시간거동에 관한 결과들을 증명하였다. [JMAA, 476 (2019) 637-664]에서는 단항시간분수계파동방정식의 초기경계값문제에 대하여 횔데르련속함수공간에서 최대정칙성에 관한 결과를 확립하였다. 그리고 [FCAA, 24 (2021) 168-201]에서는 원천항이 부지수쏘볼레브공간에 속할 때 단항시간분수계파동방정식의 초기경계값문제에 대하여 약풀이의 유일존재성을 증명하였다.
우리는 m>1인 경우에 다항시간분수계파동방정식의 초기경계값문제의 약풀이의 존재성과 점근거동을 연구하였다. 우선 라쁠라스변환을 리용하여 약풀이를 정의함으로써 초기조건과 경계조건, 원천항에 대한 약한 정칙성조건하에서 풀이의 유일존재성을 증명하였다. 다항시간분수계파동방정식의 초기경계값문제의 타당성에 관한 결과를 얻기 위하여 [AMC, 257 (2015) 381-397]에서 확립된 다변수미타그-레플레르함수의 유계성에 관한 성질을 개선하였다. 또한 방정식의 파라메터들에 관한 풀이의 맆쉬쯔안정성을 증명하였다. 마지막으로 원천항이 없는 경우에 초기경계값문제의 약풀이의 H2-감쇠평가를 유도하였다.
우리의 연구결과는 잡지 《Fractional Calculus & Applied Analysis》(Volume 25, Issue 5, (2022))에 《Initial-boundary value problems for multi-term time-fractional wave equations》(https://doi.org/10.1007/s13540-022-00080-w)의 제목으로 출판되였다.