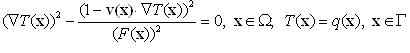《수학, 물리학, 화학, 생물학과 같은 기초과학부문에서 과학기술발전의 원리적, 방법론적기초를 다져나가면서 세계적인 연구성과들을 내놓아야 합니다.》
우리는 최근시기 지구과학, 계산음향학, 내부중력파를 비롯한 많은 분야에서 활발히 응용되고있는 이동매질에서 일반화된 아이코날방정식의 효과적인 수치풀이법을 연구하였다.
비동차이동매질에서 단조적으로 전파되는 파면의 첫 도착시간은 다음과 같은 비등방성아이코날방정식에 의해 서술된다.
이동매질에서 일반화된 아이코날방정식의 응용분야가 대단히 광범한것으로 하여 이 방정식에 대한 효과적인 풀이법이 절실히 요구된다. 선행들에서 제안된 대표적인 풀이법들로서는 특성선고속전진법과 연산자분해에 기초한 고속쓸기반복법이다. 특성선고속전진법은 이 비등방성아이코날방정식에 대한 한가지 빠르고 정밀한 풀이법이지만 이 방법은 일부 리산화파라메터에 대하여 실패하게 되며 더우기 외부흐름마당의 속도의 크기가 파면의 전개속도에 비교할만큼 큰 경우에 특성선고속전진법이 성공하는 리산화파라메터를 선택하기 곤난하다.
우리는 특성선고속전진법의 제한성을 극복하는 고속풀이법을 연구하였다. 이를 위하여 특성선고속전진법이 일부 리산화파라메터에서 실패하게 되는 리유를 구체적으로 해석하고 그 극복방도를 연구하였다. 리산화파라메터에 전혀 의존하지 않으면서 이동매질에서 일반화된 아이코날방정식의 점성풀이를 효과적으로 근사시키는 한가지 방도로서 계차수정절차를 제안하고 그에 의한 풀이법인 개선된 특성선고속전진법을 개발하였다.
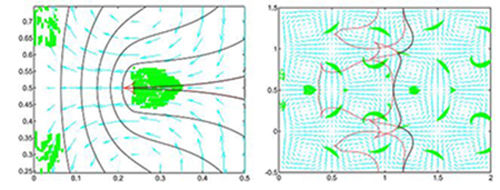
제안한 방법을 테일러-그린형회리를 가진 매질에서 전파되는 초기평면파의 첫 도착시간을 구하는 문제를 비롯한 여러 실례들에 적용하였다. 또한 우리의 방법을 리용하여 얻은 수치풀이와 경로추적법을 리용하여 얻은 풀이와의 비교를 통하여 이동매질에서 일반화된 아이코날방정식의 점성풀이를 성공적으로 근사시킨다는것을 보여주었다.
우리의 연구결과는 Springer 출판사의 잡지 《Journal of Scientific Computing》81(3)(2019)에 《Improved Characteristic Fast Marching Method for the generalized eikonal equation in a moving medium》 (https://doi.org/10.1007/s10915-019-01093-2019. 11) 의 제목으로 발표되였다.
우리의 기본수법은 일부 다른 형태의 해밀턴-야꼬비방정식의 수치풀이를 얻는데도 확장될수 있다. 우리는 현실에서 많이 리용되고있는 대표적인 5개의 해밀턴-야꼬비-벨만방정식실례들에 적용하여 좋은 결과들을 얻었다.